Determination of a Molecular Potential on a Quantum Computer
We implement the Variational Quantum Eigensolver (VQE) algorithm, simulating the potential landscape and finding the ground state energy of a hydrogen molecule.
Current supercomputers quickly approach their limit when calculating quantum properties of large molecular structures or simulating molecular reactions with high accuracy. The exponential increase in complexity of problems in quantum chemistry demands for crude approximations to make a problem more tractable for most classical calculations. Quantum computers can be used to naturally encode problems in quantum chemistry and thereby reduce computational effort. In this proof-of-principle project, we explore an algorithm suitable for noisy intermediate scale quantum devices (NISQ). The Variational Quantum Eigensolver (VQE) is a hybrid classical-quantum algorithm. The procedure can be used to estimate the low energy eigenstates and eigenvalues of a molecular Hamiltonian.

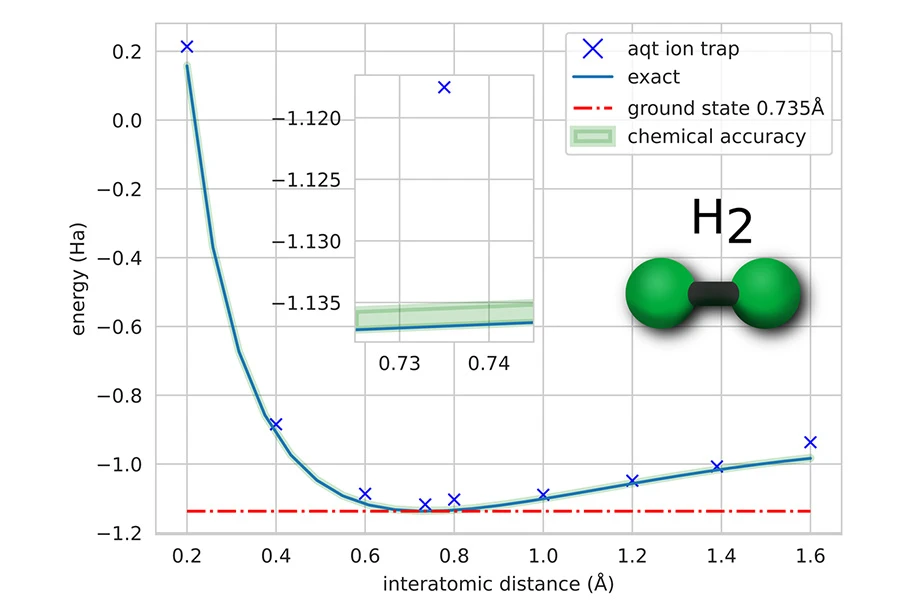
H2 ground state potential. The blue crosses represent the results obtained with the MARMOT quantum computer. The blue solid line shows the solution of the ground state energy for different interatomic distances obtained via a classical exact calculation. Here, the minimum ground state energy is highlighted by a red dash-dotted line. The green shaded area indicates the range of chemical accuracy.
Details on the Hydrogen Molecule Simulation
The Hydrogen H2 Hamiltonian can be expressed in a Pauli operator form thereby utilizing native gates of the quantum computer. The preparation of a general trial state of the VQE is formed by an RY-CNOT ansatz (see FIG 1), being a “hardware-efficient” ansatz. The angles for the initial RY rotation are at first randomly selected and adapted in each iteration step following a classical optimization procedure (NFT optimizer). For the optimization procedure, the expectation value of the Hydrogen Hamiltonian is calculated for the trial state. The expectation value forms a cost function with the rotation angles of the RY gate as its variables. From minimizing the cost function, new optimized values for the rotation angles are obtained which are employed in the next iteration step.
Results of this process are presented for a variety of interatomic distances in the main picture. Each blue cross is the result of 15 (200 shots each) VQE iteration steps, that aim to minimize the energy of the Hamiltonian for the corresponding interatomic distance (see main picture). Further details about the implementation can be obtained from https://doi.org/10.1109/QCE57702.2023.00065.
We repeated the VQE optimization for the theoretical ground state (interatomic distance 0.753Å) for different initial trial states, to get an estimate of the convergence of the results (see FIG 2). FIG 3 displays the reproducibility of the VQE runs and gives an estimate for the overall error.
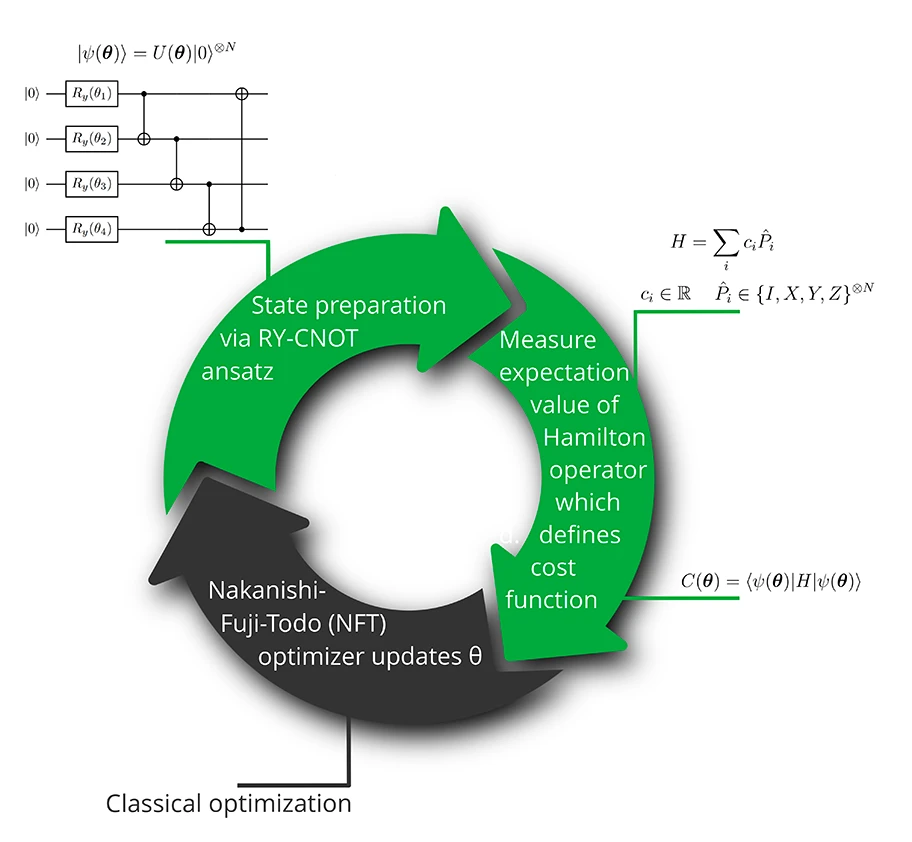
Figure 1
Variational Quantum Eigensolver (VQE) algorithm. Hardware-efficient ansatz for the state preparation circuit.
Figure 2
Ground-state energy convergence. Starting the optimization for 9 random initial trial states. The blue solid line describes the average convergence with the blue shaded area giving the deviation.
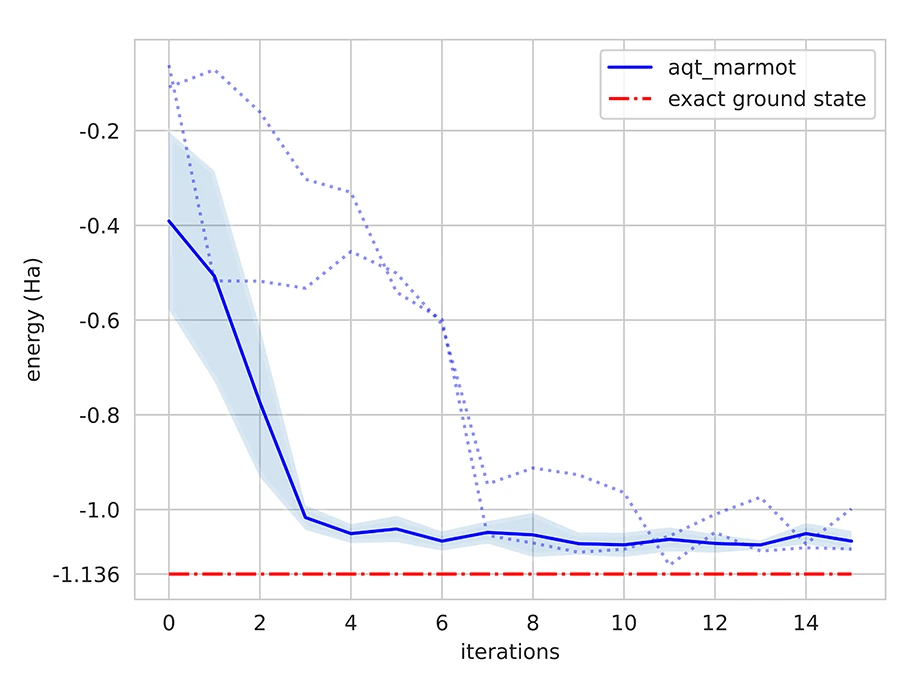
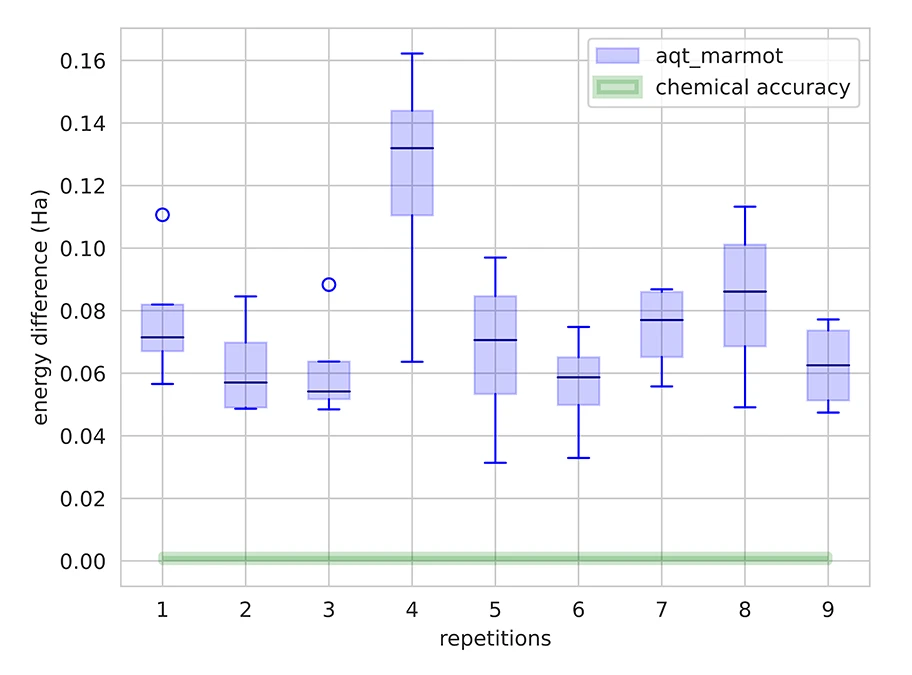
Figure 3
Ground state energy difference for 9 optimization runs, displaying reproducibility. The blue bars show the energy difference and deviations obtained from the last four iteration steps of an optimization run with respect to the theoretically known ground state value. The blue dots represent outliers.
© Photocredits: Shutterstock
