Quantum solutions find application in biochemical research
Our international joint effort between QC Ware (United States of America), AQT (Austria), Covestro (Germany) and Boehringer Ingelheim (Germany) has successfully implemented a quantum algorithm that has the capability to estimate electrostatic interaction energies of complex molecules on an AQT trapped ion quantum computer.

Driven by the vision that quantum computers can assist and accelerate the classical computation of properties of complex molecules, this work takes the scientific efforts one step further by estimating the interaction energies between large molecules in a hybrid quantum-classical approach. Although current noisy intermediate-scale quantum computers are not able to outperform classical computers, this work shows a possible path towards efficient implementations of hybrid quantum-classical algorithms. Our achievement is detailed in the scientific article Estimation of Electrostatic Interaction Energies on a Trapped-Ion Quantum Computer published in the ACS Central Science journal.
We present the first implementation of a quantum algorithm that estimates the electrostatic interaction energies between large molecules using a trapped-ion quantum computer.
The simulation of complex molecules is currently one of the most challenging computational tasks in industry. Design and development of new materials, substances, drugs, and chemical processes require well-founded knowledge of quantum mechanical properties of atoms and molecules. Due to the quantum mechanical nature of the problem, the computation is unyielding for classical computers alone. Therefore, scientists are working intensely to find better approaches in which the computationally hard part of the calculation can be outsourced to a quantum computer.
Our international team around QC Ware, AQT, Covestro and Boehringer Ingelheim developed a new hybrid quantum-classical algorithm based on symmetry adapted perturbation theory (SAPT). Together, we were able to show a successful implementation on an AQT’s trapped ion quantum computer. In this work we focused on a reduction of NO to N2O, catalyzed by a nitric oxide reductase (NOR). Using a Variational Quantum Eigensolver (VQE) approach, we generated an approximate ground state for one of two monomers on a trapped-ion quantum computer, while the other was treated with classical Hartree-Fock theory. A fermionic basis rotation at the end of the quantum computation allowed the efficient measurement of the electrostatic energy with a single quantum circuit without extension of the circuit length. The outcomes of these measurements are used as inputs for computing the electrostatic interaction energies on a classical computer.
Finally, the hybrid quantum-classical results are compared to classical Hartree-Fock and quantum mechanical complete active space configuration interaction (CASCI) calculations. Although the simulated active space is rather small due to the limited number of available qubits, the quality of the obtained results is formidable. On the one hand, the structure of the obtained output probabilities clearly resembles the structure of the noiseless simulation. On the other hand, the measured interaction energies are better compared to the classical Hartree-Fock calculations and within a chemical accuracy of 1 kcal/mol.
„It was impressive to see how the device, with only minimal error mitigation, was able to yield results for the SAPT electrostatic energy differences that were significantly better than those based on classical Hartree-Fock theory and in line with a classically exact treatment of the small model system.“
Christian Gogolin, Head of High Performance & Quantum Computing at Covestro
“In our collaboration with AQT, Covestro and QC Ware we jointly conducted an experiment on AQT’s quantum computer, marking the first time we tested our quantum algorithm for calculating electrostatic energies. The interaction with AQT’s team was both highly interactive and productive. We are proud of the results which have been published in ACS Central Science, helping Boehringer Ingelheim to be an innovation leader in quantum computing.”
Michael Streif, Project Coordinator and Quantum Computing Scientist at Boehringer Ingelheim
“We are delighted to have collaborated with AQT. Together, we explored how to use their cutting-edge ion trap quantum computer to estimate the electrostatic energy in industrially relevant but classically challenging molecules. We achieved remarkable results that exceeded our expectations. Working with the AQT team was a pleasure; their expertise and professionalism greatly contributed to the success of our project. We look forward to future collaborations and further advancing scientific frontiers together.”
Pauline Ollitrault, First author and Staff Scientist at QC Ware
The problem is first split into a quantum and a classical part, as described in Figure 1. Driven by hardware specifications, the quantum part was reduced to 4 orbitals mapped onto 8 qubits. The derived algorithm consists of 279 single-qubit gates and 63 two-qubit gates. The results obtained from the quantum measurements and the classical computations are then combined to find the electrostatic interaction energy of the system. In a next step, we use this approach to compare the electrostatic energies of two different model systems (intermediate A and intermediate B), that are characterized in Figure 2. Intermediate B differs from intermediate A in that it contains an NADH molecule in the heme pocket, whereas intermediate A does not. In this context, we are able to tell whether electrostatic interactions favor the stabilization of the NADH molecule in the heme pocket or not. As can be seen in the experimental results, depicted in Figure 3, the presence of the NADH molecule indeed leads to a lower electrostatic energy of intermediate B compared to intermediate A. Furthermore, we employed error mitigation via Zero-Noise-Extrapolation, where we extrapolate the frequencies of the observed computational states using an exponential fitting function. From the extrapolated frequencies we reconstruct the one particle reduced density matrix (1-RDM) and subsequently compute the interaction energies. Our findings indicate that the error mitigated results improved relative to the noise-free simulation as anticipated.
For more details on the theoretical procedures and the specific hardware implementation we refer the reader to our paper Estimation of Electrostatic Interaction Energies on a Trapped-Ion Quantum Computer and the Supporting Information.
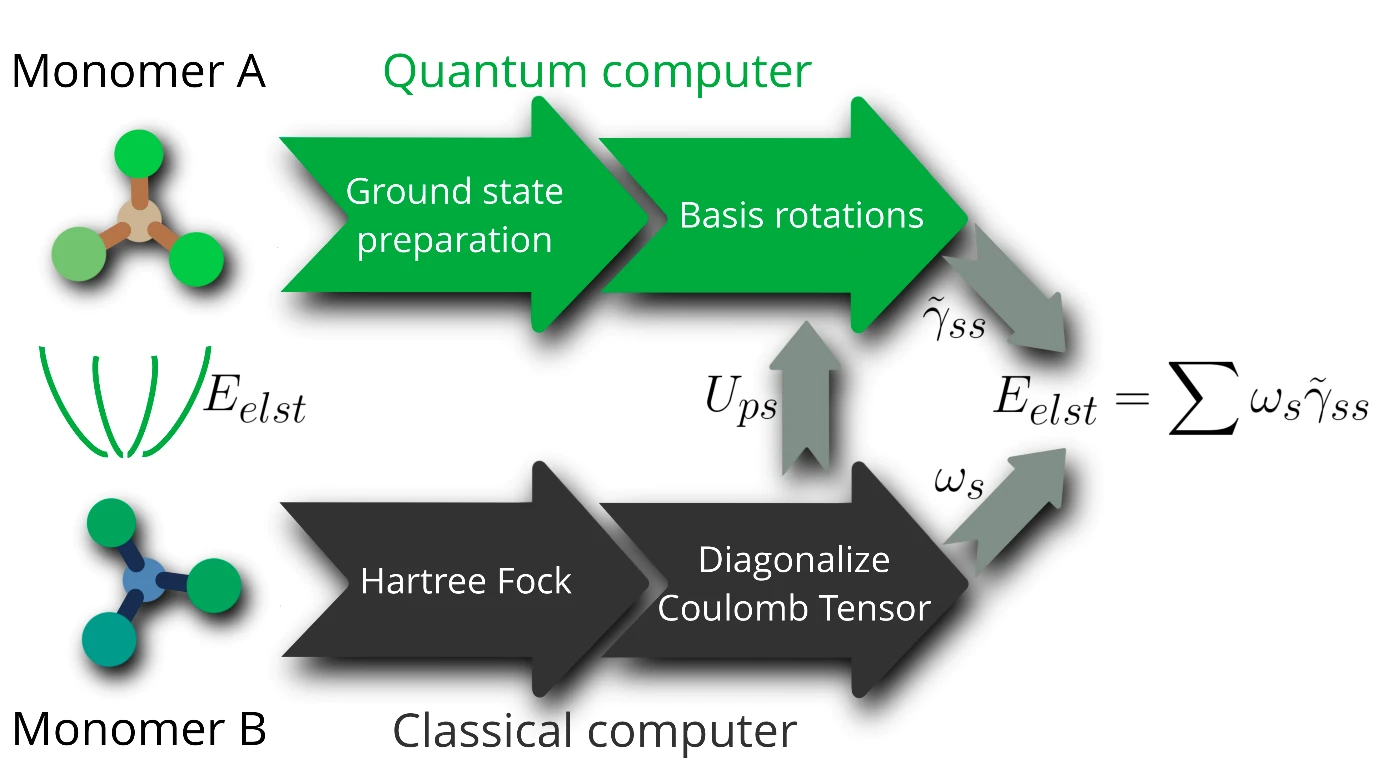
Figure 1: Hybrid quantum-classical algorithm flowchart
Estimating the electrostatic interaction energy (Eelst) between monomer A and monomer B. The quantum chemical properties of monomer B are calculated on a classical computer (black) using classical Hart-Fock simulations. The relevant quantum chemical properties of monomer A are mapped into a quantum circuit on a quantum computer (green), where the results of the classical computation are used to perform the fermionic basis rotations (Ups). The electrostatic interaction energies can now be efficiently estimated from the combination of the results of the quantum and the classical computations, where ỹss describes the measurement outcomes of the diagonal elements of the one particle reduced density matrix (1-RDM) and ωs are the eigenvalues corresponding to the precalculated basis rotations Ups.
Figure 2: Molecules (Monomeres)
We compare the electrostatic energies of two systems, intermediate A (orange boxes) and intermediate B (green boxes). Left: In intermediate A, monomer A (blue) consists of three surrounding amino acids and water molecules. In intermediate B, monomer A (blue) consists of three surrounding amino acids, water molecules and a NADH molecule. In both cases, monomer B (black) includes the NO-bound heme. Right: We illustrate the four orbitals in the active space of monomer A for intermediate A labelled as model A and for intermediate B labelled as model B. The goal is to find out, whether the electrostatic interaction energy is lowered by the presence of the NADH molecule or not.
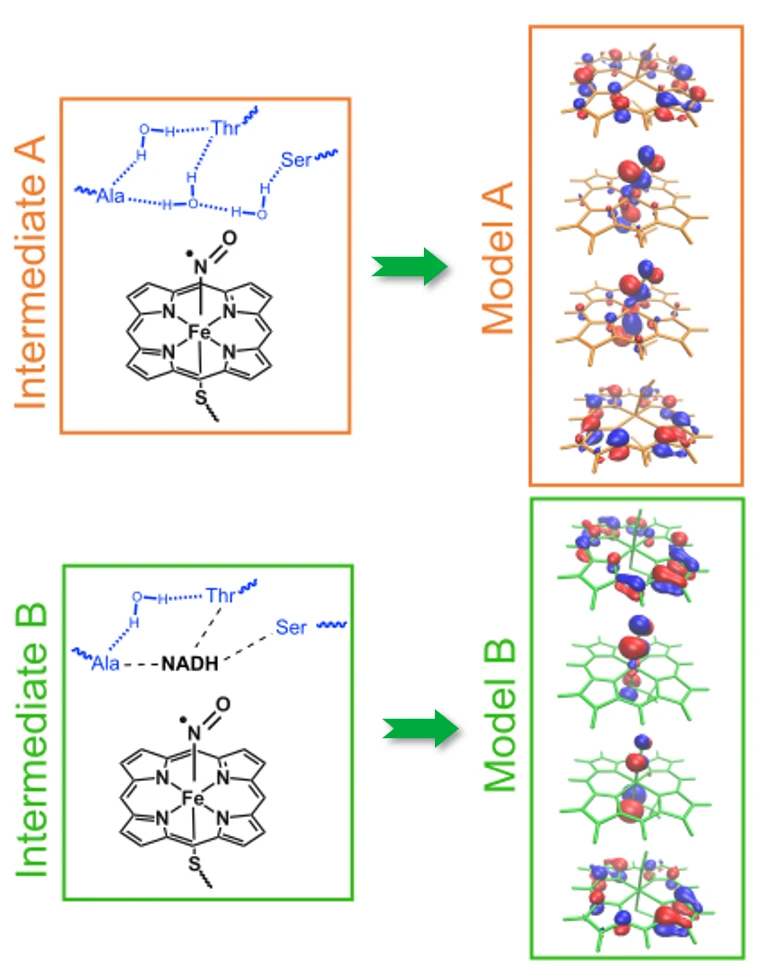
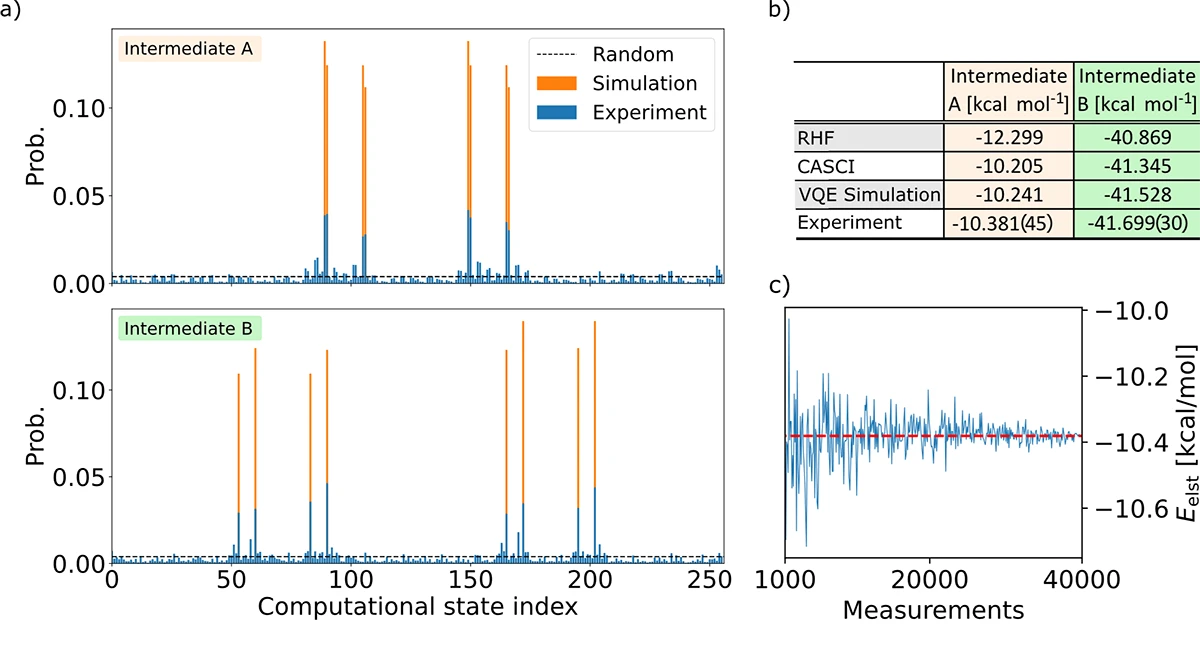
Figure 3: Experimental results
In a) we present measurement results that are obtained from an AQT quantum computer (blue). For comparison, we illustrate the ideal results (orange), as calculated from a noiseless simulation. The experimental results clearly resemble the structure of the ideal simulation and provide good estimates for the electrostatic interaction energies. In b) we compare the experimental results to classical Hartree-Fock (RHF) and quantum mechanical (CASCI) calculations. For both intermediates the experimental results are closer to the reference CASCI result compared to the classical RHF calculations. In c) we illustrate that the estimate of the electrostatics for intermediate A quickly converges with increasing number of measurements.
© Photocredits: AQT/Helene Hainzer
