Simulating material properties with cloud-based quantum technology
Quantum simulations are well-suited to explore material properties, potentially leading to the discovery of new classes of materials with unique qualities and therefore revolutionizing various industries such as electronics, chemistry and manufacturing.
The German IT service provider System Vertrieb Alexander GmbH (SVA www.sva.de) employs an AQT quantum computer to simulate macroscopic properties of a magnetic system, demonstrating the potential of quantum computers for material simulations.

© Photocredits: AQT/Helene Hainzer
The diverse physical properties of various materials play a crucial role in science and engineering. Experiments in laboratories are costly and classical computers fall short in simulating microscopic systems. Using quantum computers for simulating material properties promises a huge potential because their inherent utilization of quantum effects makes them the perfect candidates to simulate quantum systems efficiently.
Building and operating quantum hardware is complex, expensive, and requires controlled environments. AQT’s cloud service ARNICA provides access to our quantum computer systems, allowing users to perform quantum computations without the need to own or maintain a quantum machine themselves.
In a collaboration with System Vertrieb Alexander GmbH (SVA), we employ AQT’s quantum computer system IBEX Q1 to simulate a complex magnetic system. We implement a simple but illuminating model to observe how the overall magnetisation of a quantum system develops with time.
Model Formulation
Magnetic systems are all-around us, but explanation of their behaviour and effects requires sophisticated models due to their large sizes and the long-range nature of the magnetic force. One of the simplest models for magnetism is the one-dimensional Ising model, which consists of spins (imaginable as little magnetic bars) located on a chain. The spins interact with their nearest neighbours and with an additional transversal external field. The two constants J and h represent the strength of the interaction between each two neighbouring spins and between the external field and each spin, respectively:

To describe the system from a mathematical point of view, we use a Hamiltonian which takes into account all interactions:
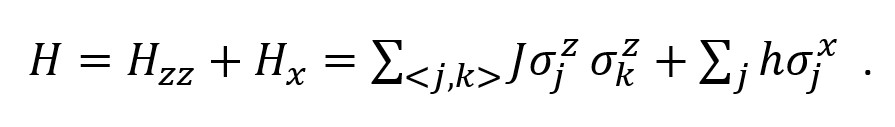
The time evolution of the system is then described by the Schrödinger equation.
The magnetisation of a magnetic system describes the measure of alignment of its individual parts. The maximal magnetisation is reached when the spin of each individual element aligns along one direction. We talk about minimal (or even zero) magnetisation when all the spins are randomly oriented while averaging out their individual contributions to the macroscopic magnetisation.
In this project, we measure the final magnetisation of an initially maximally magnetised Ising chain in an external transversal magnetic field after it has evolved for a given time. To investigate how the system behaves under different conditions, we measure the final magnetisation for various values of the coupling strength J between the spins.
Circuit execution, challenges and results
A quantum computer based on trapped ions seems to be the ideal candidate for such calculations. After applying approximation schemes, the resulting quantum circuit for an 8-spin Ising chain is shown in figure 1. Technical details to the model formulation and approximations are summarised here: See here for technical details. In the direct and unprocessed experimental results the expected features are suppressed, since all first-generation quantum devices are error-prone. Nonetheless, such errors can be mitigated using methods like zero-noise extrapolation, to an extent that allows us to obtain improved results. To implement the method, we utilize the open-source error-mitigation software mitiq (https://github.com/unitaryfund/mitiq) and apply it to our measurements.
The remaining challenges are the depth of the quantum circuit, the number of experimental repetitions to obtain statistically significant results and the long-term stability of the quantum hardware resulting in unwavering computational quality. All three challenges are well mastered by AQT’s quantum computer IBEX Q1, which features a Quantum Volume of 128, a duty cycle of >20000 quantum circuits per hour sent and retrieved over the cloud and an outstanding stability of the computational quality thanks to automated recalibration.
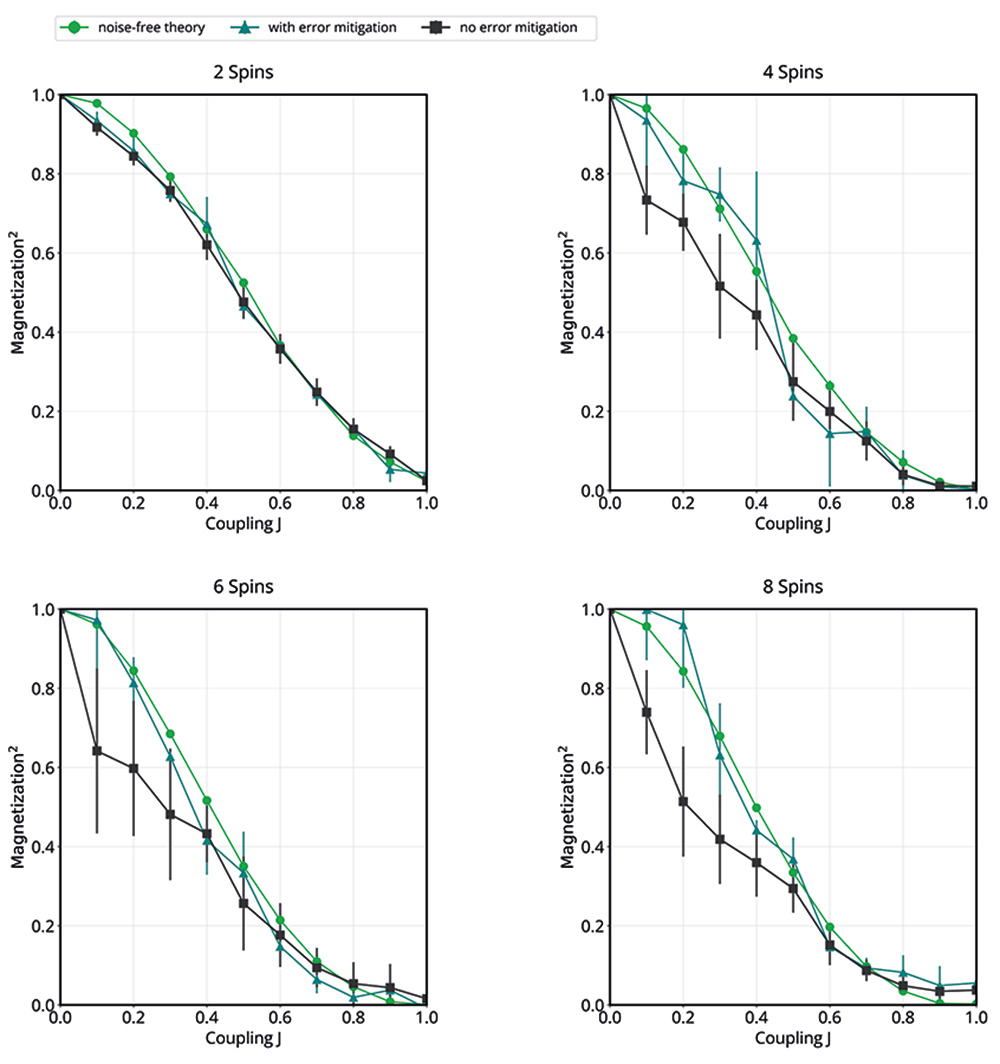
Figure 2 shows the second power of magnetisation for different numbers of qubits, i.e. spins, in dependence of the coupling strength . The green dots refer to a noise-free theoretical simulation of the trotterised problem which we use as the baseline. Furthermore, the green triangles and black squares correspond to the experimental simulation on the quantum system with and without error mitigation, respectively. Comparing the results for different qubit numbers, we see an improved performance when error-mitigation is applied.
The negligible difference between error-mitigated and non-mitigated results for the 2-spin experiment reflects the high fidelity of the IBEX Q1 single- and double-qubit gates. The difference increases with the number of spins as the depth of the circuit grows with the qubit count. For deeper circuits, the qubit coherence times start to play a role and affect the results as an additional source of error.
Using the error-mitigation technique we were able to reproduce the expected behaviour of the 8-spin system demonstrating small overall gate errors and great qubit control. The present results reveal great potential for future development and applications.
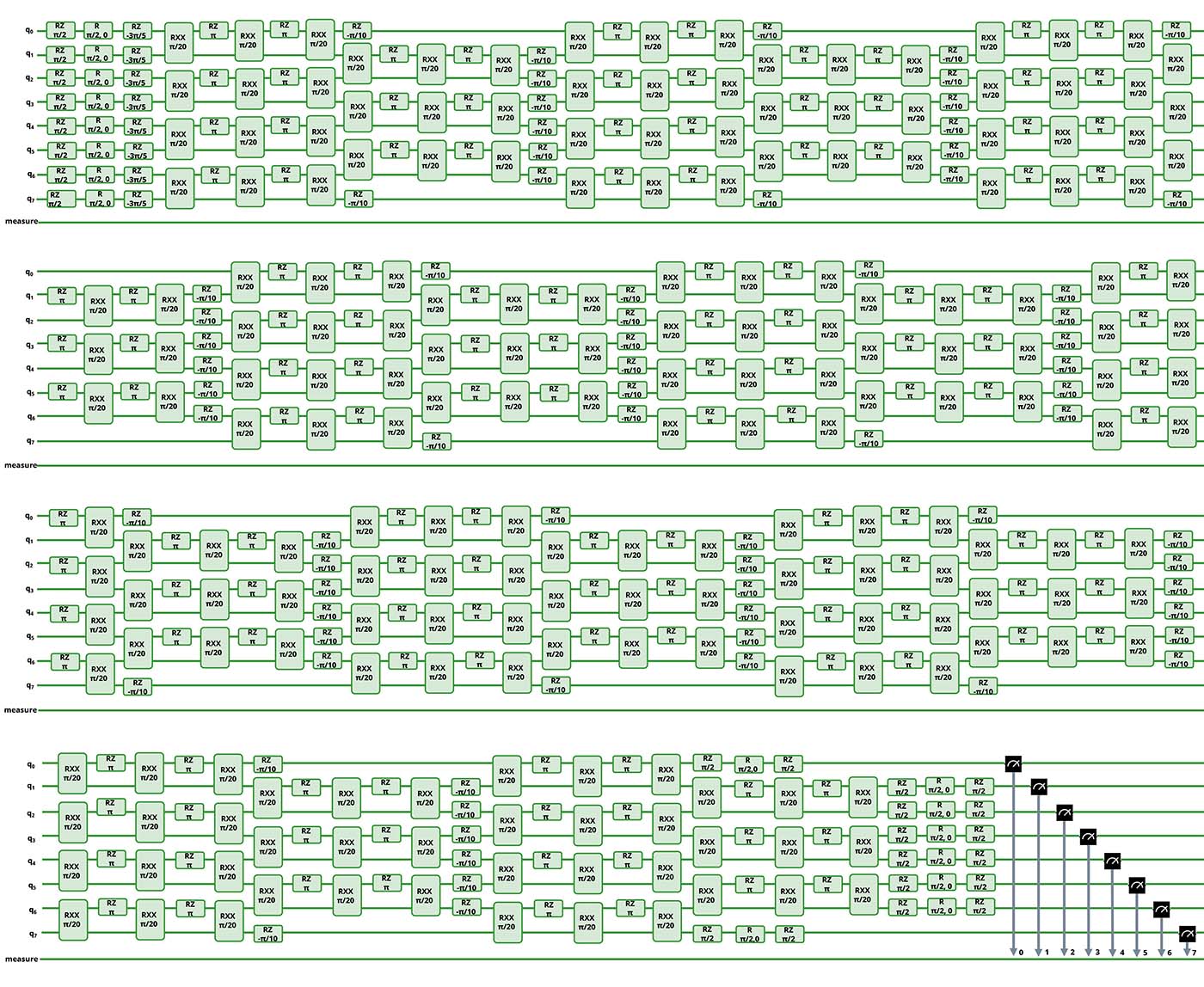
Figure 1: Quantum circuit
Quantum circuit for the simulation of a magnetic system on 8 spins, at coupling strength J=0.5 and with error mitigation. The circuit counts 471 gates.
Figure 2: Results
The second power of magnetisation for different number of qubits (= spins), in dependence of the coupling strength J . The green dots refer to a noise-free theoretical simulation of the trotterised problem, the green triangles and black squares correspond to the calculation on the quantum system with and without error mitigation, respectively.
“AQT is one of the very few European quantum computing manufacturers who are open to close collaboration with industrial partners and allowing a transparent assessment of their products even in the early stage of the development”, says Christopher Zachow, Head of Competence Center High-Performance & Quantum Computing at SVA.
„It is a pleasure to tightly work together with an innovative partner such as SVA to develop early quantum computing capabilities and their applications in materials science,“ adds Juris Ulmanis, Director of Quantum Technologies at AQT.
Disclaimer:
Co-funded by the European Union project QCDC, No. 190118992. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or European Innovation Council and SMEs Executive Agency (EISMEA). Neither the European Union nor the granting authority can be held responsible for them.

